K-means Clustering for Lateral Movement Detection

Alicja Dobrzeniecka & Marvin Straathof @

Oct 31, 2023 10:53:46 AM

In the ever-changing landscape of cyber security, detecting lateral movement within a network is a significant challenge for security professionals. Lateral movement refers to the movement of cyber attackers within a network after gaining initial access to a single system. To limit the spread of an attack within an organisation and reduce the potential impact, detecting lateral movement is critical. Because we have large amounts of data in cyber security, we can apply machine learning methods to improve the automatic detection of malicious events. The aim of this article is to demonstrate how this can be done, in this case by using a K-means clustering algorithm to detect anomalies in unlabelled network data.

In many cases, cyber data is unlabelled, which presents a challenge in terms of how to model and evaluate it. For the problem of anomaly detection we can then use historical data to model 'normal' behaviour in a network. As a result, an unsupervised model of choice can potentially detect new malicious samples as they probably deviate from what has been observed in the past.

K-means blog

Since we have some prior ideas about the network, namely that there are likely to be some clusters that can be categorised based on device type, connection, etc., we choose a clustering approach as a starting point. In this blog post, we show one of the simplest approaches to the problem of anomaly detection in an unsupervised setup. We show how you can use the K-means clustering algorithm to detect malicious lateral movement connections in a network.

Our goal is to identify clusters that share certain similarities, such as hostnames they connect to, device types, destination ports, and so on. If we collect a good representation of the historical data and extract the features correctly, we may end up with a model that allows us to detect anomalous events because they differ from the historical data patterns.

Detect anomalous connections in a network

In this section we present our first attempt to automatically detect whether a new sample is anomalous or not, based on historical data. We start with a list of assumptions that we have made in order to keep the scope of the project feasible and to provide a first proof of concept. We then give details of our implementation. Finally, we point out known challenges and limitations of clustering methods for anomaly detection. We conclude this section with our ideas for future improvements.

A/ Assumptions

For our proof of concept, we limited the scope of the data to only those connections that included the destination port of our choice. In our case, this was port 445, which is used by a Server Message Block (SMB) protocol, but any port of choice could work if there was sufficient data.
We focused only on internal network connections (excluding Internet connections).
The samples come from either servers or clients.
We consider the K-means implementation as a first proof of concept for anomaly detection in a network and not as a final solution to the problem.

B/ K-means algorithm

K-means is an iterative clustering algorithm that aims to divide a dataset into K distinct clusters. You must specify a number of clusters, then the algorithm starts by randomly selecting K initial cluster centres, assigns each data point to the nearest centre, recalculates the new cluster centres based on the assigned points, and repeats these steps until convergence is reached. K-means attempts to minimise the sum of the squared distances between data points and their assigned cluster centres.

C/ Implementation

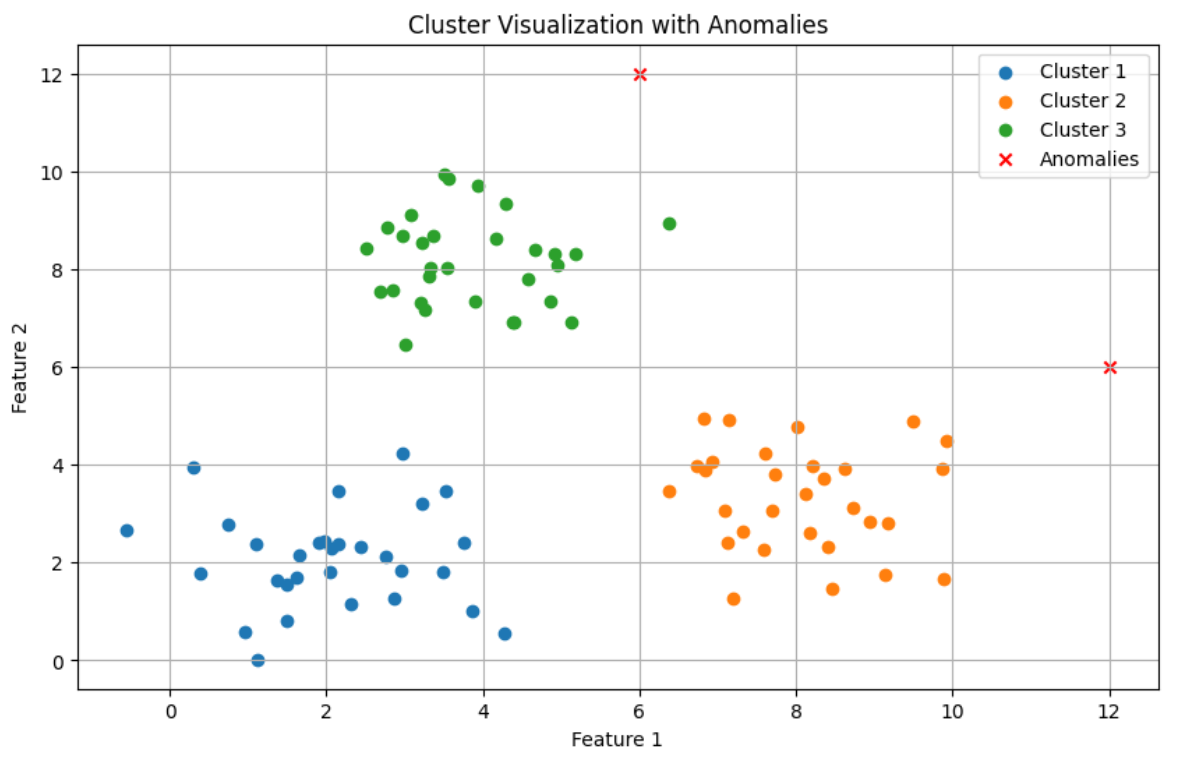
image-20230816-101416

Visualisation of example anomaly detection with clustering. Points that are far from any of the clusters are considered anomalous.

For our first proof of concept we did the following things:

[Collect and sort data] We collected the data and divided it into proper sets: train, test and validation. If you do not have access to real network data, you can use one of the public datasets (eg. Data Sets - Cyber Security Research).
[Clean data] We cleaned and filtered the data.

a) We had to deal with the problem of missing values. We decided to remove the samples with missing critical fields for the time being, but we may approach this differently in the future.

b) We kept the samples that matched our assumptions, meaning that they are from the internal network and have port 445 as the destination port as this is the port that the SMB protocol uses.
[Prepare features] We prepared the features, mainly by looking eg. at the hostnames, destination port and IP and counting the number of incoming or outgoing connections. We also drew on the knowledge of domain experts when exploring the available features.
[Standardize] We used standardization for numerical features. One of the reasons for this is that K-means clustering is based on calculating distances between data points, so by standardizing the features we ensure that each feature contributes equally to the distance calculations. If we do not do this, there is a risk that features with larger ranges will have a greater impact on the distance calculations than those with smaller ranges.
[Dimensionality reduction] To ensure that K-means clustering is interpretable and to reduce noise and computational cost, we applied a dimensionality reduction method. We encoded categorical data using Multiple Correspondence Analysis (MCA) and then applied Principal Component Analysis (PCA) to reduce the overall dimensionality. However, there are a number of other methods available that can be selected depending on the situation and we have not tested all available ones, only the most common (like UMAP).
[K-means] We applied K-means with a number of centroids that we found to be the most appropriate within the given metrics. You can determine their number by using the elbow method or silhouette score on your data. We treated our historical data as data representing 'normal' behaviour (as we verified that there were no incidents in a given time period). To detect anomalous samples, we did the following:

a) We took a mean of each cluster and its corresponding standard deviation.

b) We set a threshold above which the new sample should be considered anomalous.

c) Anomalous in this case means a sample that is too far from any of the clusters (e.g. more than two standard deviations from a given mean).
[Evaluation] After successfully training a model, we evaluated it on new samples to see how efficient it is at correctly labelling new samples as normal or abnormal.

D/ Challenges and limitations

This approach should be seen as an initial proof-of-concept that can be improved upon. There are known limitations that can happen and should be taken into account:

[False positives] An anomaly does not necessarily have to be malicious. If a new device appears on a customer's network that is benign, but its connections deviate from the historical behaviour of a network, then that sample can potentially be flagged by a model as something suspicious. The false positive rate is something that needs to be decided. What is the acceptable number per day so that it is feasible for analysts to investigate the alerts?
[K-means sensitivities] K-means itself has a number of limitations. It is sensitive to the initial choice of centroids, it is sensitive to the outliers in the data, and the choice of cluster numbers must be known in advance. As mentioned before, it can be determined with, for example, the elbow method.
[No single criterion] There is no single criterion that measures how well the clusters reflect the “correct” real world division. One of the methods of measuring the quality of clusters is average Euclidean distance from a cluster’s centroid to the members of a given cluster.
[Misleading conclusions] One needs to be careful with the outcome of the method. Even if the data is not suitable for clusters, the algorithm will still return clusters which can lead to misleading conclusions about the data. To get better idea whether the clustering is suitable for a given data you can inspect the data visually to see if any clustering naturally emerges. You can also check Hopkins statistic to determine if the data has a clustering tendency.
[Linear decision boundary] The decision boundary in K-means clustering is linear which can be considered a drawback when dealing with datasets that have complex non-linear structures.
[Evaluation] Evaluating the model is difficult because real malicious events are very rare. You can artificially create a set of samples that are similar to the training set and represent different connections to evaluate the ratio of true positives, false positives, true negatives and false negatives.
[Simplistic approach] The approach itself is very simple and can be naive in some cases. Using mean and standard deviation to detect anomalies means that we are assuming a Gaussian distribution, the model is sensitive to outliers and we may not be able to capture more complex patterns.

E/ Future Improvements

Expanding the evaluation set to ensure that the model can correctly capture less obvious malicious connections.
Optimising hyperparameters for dimensionality reduction methods, eg. using Optuna - A hyperparameter optimization framework
Trying more complex models that can better capture "normal" behaviour. One option would be to use the Gaussian Mixture Model or Variational Autoencoder (VAE) model.
- An example of how Gaussian Mixture Model can be applied to anomaly detection can be found in the article Deep Autoencoding Gaussian Mixture Model for Unsupervised Anomaly Detection.
- One of the applications of VAE for detecting anomalous behaviour can be found in the paper Variational autoencoders for anomaly detection in the behaviour of the elderly using electricity consumption data.

Conclusions

In this blog we have shown a simple first approach to anomaly detection with unlabelled network data. We start with something simple, with the goal of improving it with more complexity in subsequent iterations as the data and scope are better understood. Such an approach allows us not to get stuck in a problem space that is too complex at the beginning, but to slowly move from simple and sometimes naive methods to more complex ones as we learn more about the data and the domain itself.

It is worth noting that there are many challenges and limitations at each step in the process of building a model to detect anomalous behaviour. Among other things, if the original data is not labelled, we have a challenge in evaluating the final solution. We can artificially generate some samples to verify the behaviour of the model, but until there is a real malicious event, we have no guarantee that it will be captured by a model. Furthermore, the model itself may be sensitive to initial choices of parameters and random factors. We should be aware of the limitations of the solutions we have, so as not to overestimate their promise.

In our approach, as we were just getting to know the problem space, we narrowed the scope of our project to make it a feasible challenge. Narrowing the scope can be a helpful step for the first proof of concept and getting to know the data. After a first experience with simple assumptions and limited scope, we have many ideas for further improvements. We can now expand our scope to tackle more problems at once, for example in our case, to focus on more than one protocol. Therefore, if the data seems quite challenging, we recommend starting with a small but self-contained project and then moving on to more complex methods and a larger scope.